Topcoder Single Round Match 616 Div 2 T3 题解

题目大意

给你一个 N×M 的字符矩阵，代表 N 行 M 列的点。每个点可能是 # 或者 . （“障碍”与“空白”）。现在你要从中选出一些空白点使得它们构成两个 “L” 形状（即选出两条只有一个交点的线段组成）。有如下规定：

最后你需要在一幅图里找出两个 “L” 形状，并且这两个 "L" 不能有任何相交（即不可以占用公共的点）。问你有多少种方案。

题目里的字符矩阵以 vector <string> grid 给出。注意本题的时限是 3 秒。

  • grid will contain between 2 and 30 elements, inclusive.
  • All elements of grid will contain the same number of characters.
  • Each element of grid will contain between 2 and 30 characters, inclusive.
  • Each character of grid will be either '.' or '#'.
  • Time limit (s): 3.000
  • Memory limit (MB): 256

题目原文

Please note that this problem has a non-standard time limit: 3 seconds.

A yet unknown "LL Company" wants to design a logo. After a long discussion, company designers decided that the logo should consist of two letters L drawn in some way.

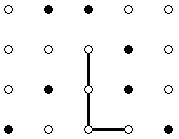
To start with something, designers drew N rows of M points each, one under another, so that these points form a rectangular grid. They also painted each point either white or black. Here is an example of what they could get for N = 4 and M = 5:

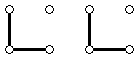
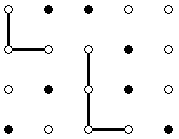
Designers agreed to draw each letter L as a union of a horizontal and a vertical line segment intersecting at their left and bottom ends, respectively. The segments must have positive lengths, and their endpoints must be white grid points. All grid points that lie on the segments must be white as well. For example, here are two valid placements of a letter:

233333

Note that neither the letters nor the grid can be rotated.

The final requirement is that the two letters should be disjoint. That is, no white point should lie on two segments belonging to different letters.

You are given the grid with N rows and M columns, encoded as a vector grid with N elements, each containing M characters. Each character is either '.' or '#', meaning that the corresponding point is either white or black, respectively.

Return the number of different possible logos with two L's drawn on them according to the requirements. Two logos are considered different if there is a pair of points that is connected by a line segment in exactly one of the logos.

样例解释

样例零：

{"....",
 "...."}

Returns: 1

样例一：

{".##..",
 "...#.",
 ".#.#.",
 "#...#"}

Returns: 3
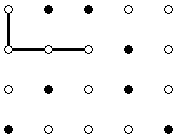
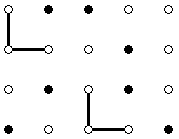
This is the example from the problem statement. The three possible logos look as follows:

样例五：

{"##############",
 "##############",
 "#.############",
 "#.############",
 "#.############",
 "#.############",
 "#.############",
 "#.############",
 "#.#####.######",
 "#.#####.######",
 "#.#####.######",
 "#....##.######",
 "#######.######",
 "#######.######",
 "#######.######",
 "#######.######",
 "#######.######",
 "#######.######",
 "#######......#",
 "##############"}

Returns: 1350

这幅图里只有两个 L 形状的“基准点”（即拐角），所以方案数量就是几条线段长度可能数量之乘积。
9×3×10×5=1350。

……

分析

一开始我们肯定可以想到一个 $\Theta (N^4\ast M^4)$ 的想法：枚举第一个 L 的左下角的点（以下我们称之为“基准点”），然后向上、向右枚举，累计所有情况。

然后我们可以发现，“向上、向右枚举”的过程可以免去，可以先构造数组 up[i][j] 和 rght[i][j]，分别表示点 (i,j) 向上、向右有几个白色的点。对于两个基准点 (i,j) 与 (k,t)，方案数就是 up[i][j]*right[i][j]*up[k][t]*right[k][t]……是吗？

但是我们又发现了问题：如何判断两个 L 是否相交呢？在刚才直接向上、向右枚举的时候我们可以方便地判断相交，但是现在我们这样的方式，就需要分以下几种情况讨论了：

XOXOX \\
XOXOO \\
XOXXX \\
XOOOX \\
XXXXX
XXXXXX \\
XOXXXX \\
XOXOXX \\
XOOOOX \\
XXXOXX \\
XXXOOO

如果按前面两个 L 分别相乘计算势必会有重复，这时只要减去相交的一部分的重复情况就可以了。

复杂度 $\Theta (N^2\ast M^2)$，考虑细节有点麻烦。

代码

#include <bits/stdc++.h>
#define CLEAR(_) memset(_,0,sizeof(_))
#define CLEAR_MAX(_) memset(_,0x3f,sizeof(_))
#define CLEAR_MIN(_) memset(_,0x80,sizeof(_))
#define CLEAR_REG(_) memset(_,255,sizeof(_))

using namespace std;
const long long maxn=35;
long long n,m;
long long rght[maxn][maxn],up[maxn][maxn],ans;
vector <string> a;

template<class T> void checkmin(T &a,const T &b) { if (b<a) a=b; } 
template<class T> void checkmax(T &a,const T &b) { if (b>a) a=b; }
class TwoLLogo {
public:
    long long countWays( vector <string> grid ) ;
};

inline void init(){
    ans=0;
    CLEAR_REG(up);CLEAR_REG(rght);
}
inline void Build(){
    for (long long i=0;i<n;i++)
    for (long long j=m-1;j>=0;j--) if (a[i][j]=='.'){
        up[i][j]=i==0?0:up[i-1][j]+1;
        rght[i][j]=rght[i][j+1]+1;
    } else up[i][j]=rght[i][j]=-1;
}
long long TwoLLogo::countWays(vector <string> grid) {
    init();a=grid;
    n=grid.size();m=grid[0].length();
    Build();
    for (long long i=0;i<n;i++)
    for (long long j=0;j<m;j++) if (a[i][j]=='.')
    for (long long k=0;k<n;k++)
    for (long long t=0;t<m;t++) if ((a[k][t]=='.')&&((i!=k)||(j!=t))){
        if ((up[i][j]==0)||(rght[i][j]==0)||(up[k][t]==0)||(rght[k][t]==0)) continue;
        if ((i<k)&&(j>t)) ans+=rght[i][j]*up[i][j]*rght[k][t]*up[k][t]; else
        if ((i<k)&&(j<t)) ans+=max((long long)0,
            up[i][j]*rght[i][j]*min(up[k][t],k-i-1)*rght[k][t]+
            up[i][j]*min(rght[i][j],t-j-1)*up[k][t]*rght[k][t]-
            up[i][j]*min(up[k][t],k-i-1)*min(rght[i][j],t-j-1)*rght[k][t]); else
        if ((i<k)&&(j==t)) ans+=up[i][j]*rght[i][j]*min(up[k][t],k-i-1)*rght[k][t];
        if ((i==k)&&(j<t)) ans+=up[i][j]*up[k][t]*min(rght[i][j],t-j-1)*rght[k][t];
    }
    return ans;
}